 |

Submitted by , posted on 09 May 2002
|
 |
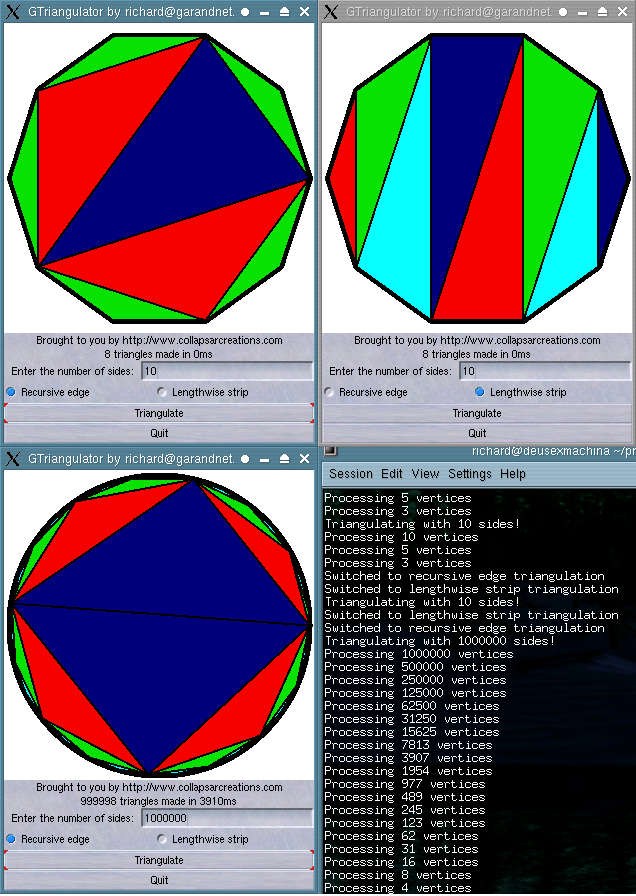
Image Description, by

This is a program I wrote to test two algorithms for reducing polygons to
triangles. The algorithms will work for any convex polygon with three or more
sides. The images on the top show two algorithms used on the same polygon,
and the images on the bottom show the results of a million-sided polygon with
the first algorithm (although the low resolution hides a lot of edge detail)
and the progress of the recursive processing. I came up with these algorithms
for a model converter for the game I'm working on.
Both algorithms have the same input: a list of vertices. The vertices must be
in order, and both algorithms will produce triangles with the same winding as
the original polygon if used properly. If you want to implement one of them,
I found it very convenient to make a copy of the first vertex at the end of
the list.
The first algorithm is the "recursive edge" algorithm. It works by making
triangles around the edge (vertices 1 to 3, 3 to 5, etc), making a list of
the endpoints of those triangles and any unused vertices, and calling itself
again on that list. In this program, it changes color each time it recurses -
as you can see, it takes three levels to process a 10-sided polygon. The
million-sided polygon looks like it only takes 4 levels, but that's because
it only cycles through 4 colors - it really takes 19 levels of recursion to
process.
The second algorithm basically produces a triangle strip. This one is much
simpler: it takes the first vertex to start off the triangles, then splits
the rest of the list in two. The first list is vertices 2 to (n / 2) + 1, and the
second list is vertices n to (n / 2) + 2. After starting off with the first
vertex from each list, it alternately takes vertices from each list to make a
"triangle strip". It changes colors at each triangle, so you can see the
progress.
The full source code of the program and a readme with more detail are
available at http://www.collapsarcreations.com/dl.php, at the bottom. I wrote
it in Linux, but since it uses GTK it shouldn't be too hard to compile in
Windows.
|
|

