The feature of Plücker coordinates which attracted me most was the
simplicity of testing ray-polygon intersections [2]. If all the edges of a
polygon are converted to their Plücker representations (taking care to order
the vertices in the same direction) then taking the permuted inner product of
the ray with each edge we can determine whether or not the ray passes through
the polygon. For the ray to pass through the polygon, all the products must
agree in sign (or one product, max two, must be zero, and the others must
agree.) In the following diagram the edges move counterclockwise around
the intersecting ray.
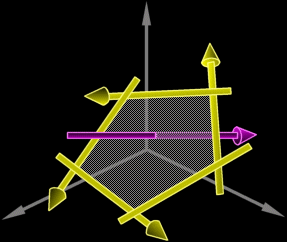
We can go further to compute the point of intersection with a
triangle or a quadrilateral, if an intersection did occur. Consider a triangle
with edges 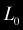 , ,
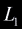 , , 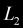 ,
where ,
where 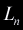 is the edge opposite to the nth vertex. Take the ray
is the edge opposite to the nth vertex. Take the ray 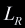 and its products with edges
and its products with edges 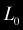 , ,
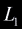 , , 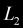 ,
being ,
being 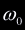 , ,
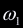 , , 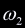 respectively. If their signs agree, we know that an intersection occurred. It
turns out that these are the unnormalized barycentric coordinates for the point
of intersection. If we take the normalization factor to be
respectively. If their signs agree, we know that an intersection occurred. It
turns out that these are the unnormalized barycentric coordinates for the point
of intersection. If we take the normalization factor to be 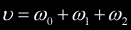 then the normalized barycentric coordinates are:
then the normalized barycentric coordinates are:
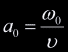 , , 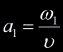 , ,
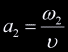 . .
Now the point of intersection in Cartesian coordinates is the
linear combination of the vertices 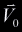 , ,
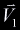 , , 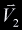 . The point of intersection,
. The point of intersection, 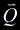 ,
is then ,
is then
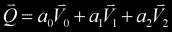 . .
The same method can be extended for testing for intersections of
rays and convex volumes (e.g. a cube). The ray needs to intersect at least one
face of the volume in order to intersect with the volume. The ray-polygon test
can be optimized, however, because each edge is shared. Only one permuted inner
product is therefore necessary per face.
|


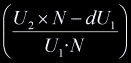



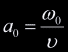 ,
, 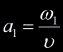 ,
,
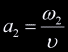 .
.

