|
The Art of Demomaking - Issue 06 - Bitmap Distortion by (27 September 1999) |
Return to The Archives |
Introduction
 |
|
I won't waste time with whitty introductions this week since we have a lot to learn ;) So lets get down to business... In this tutorial you will find out how simple bitmap distortion is, and how you can drastically increase visual quality by performing bilinear filtering. I will also tell you about cache efficiency. |
Distortion
 |
|
So far for every pixel we have drawn, we used information from a corresponding index in another buffer. The idea behind distortion is that we use a two dimensional displacement to access the other buffers. The easiest effect that uses displacement simply involves copying a pixel from a displaced location: distortion.
Just like for the plasma, we can precalculate much more if the two displacement functions remain constant over time. Again, we simply translate the functions instead. So two extra buffers are needed to store the two displacement functions. Note that no range checking is performed, so if any of the displaced coordinates x or y are too big, the image will wrap around. The program may even hang. This can be fixed by either adding clipping, or precalculating both displacement functions carefully. |
Bilinear Filtering
 |
|
Now you may notice our variables x and y in the algorithm above are both integers. This means that any distortion we introduce is rounded to the nearest pixel. This can produce some disappointing results when the distortion is close to zero. A solution is to introduce bilinear filtering. You've probably all heard of bilinear filtering for textures applied to 3D polygons. This is really quick when done in hardware, but our aim will be to make sure we can get it quick in software. Here's the theory behind bilinear filtering. Say we have the coordinates of a texel (pixel from a texture) available in floating point. We could just round those values, and load the nearest texel. That would be quick, but not as accurate as it could be. What we do is find the 4 closest texels, and linearly interpolate their colour values in both directions. And voila, we get bilinear filtering. 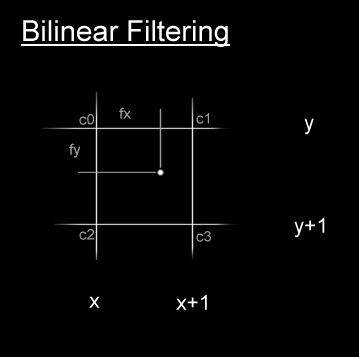 This is what the equation to get the bilinear filtered value looks like. A few simplifications are possible, but i'll leave that to you.
The output quality is greatly enhanced by bilinear filtering. When you get used to it, it's hard to do without it. But the obvious major draw back is speed. We have to load 4 times more bytes from memory, and multiply them together. Even with low precision fixed point, the demo is about twice slower with bilinear filtering... which is acceptable I suppose. |
The Down Side
 |
| As you may have noticed, the computation required to distort an image (even without bilinear filtering) is slightly higher than just copying. An extra multiplication and a couple of additions per pixel are needed. But the speed lost in processing is however insignificant compared with the draw back of not addressing the memory in consecutive order. I was going to talk about cache at a later date, but since there's not much more to say about distortion, I'll cover that topic now. |
The Cache
 |
|
The cache is a intermediary buffer between the processor's registers, and the main memory. I always think of the cache as a "wannabe". It wants to be as quick as the registers, and as big as the main memory. But it ends up slower but bigger than the registers, and quicker but smaller than main memory. The main reason of course being production costs, since the technology is available. The following few paragraphs will explain the way the cache works. I should point out that this is transparent to the program, which means you don't need to worry about it since it's all done automatically. When your program reads a byte from memory, it's address is checked by the cache. Different types of caches check this address in various ways, but they all have the same result. I won't go any deeper into that explanation since it's irrelevant to our bitmap effects. After the address is checked, if the required byte is in the cache, you get a cache HIT. This means the required byte is found, and doesn't need to be loaded from main memory. If this byte byte is not found inside the cache, a sequence of bytes (starting from the byte in question) must be loaded into one line of the cache. A line of cache is just a sequence of bytes, it's size depending on your processor, but usually 256 long. The process of loading some bytes from main memory into the cache is quite slow, and is called a cache MISS HIT. The time penalty is a couple of cycles, depending on the memory's performance and clock speed. That delay sounds reasonable, but when repeated, can significantly slow down a program. And that's the problem we run into with our distortion program. Without distortion the program reads bytes from memory linearly, which exploits the cache to it's full potential. When we introduce distortion, the higher the displacement the lower the probability is of getting a cache hit. This problem is most apparent if you rotate the bitmap 90 degrees. Apart from the stupid solution of using low intensity or no distortion at all, a common solution (introduced by Pascal / Cubic Team) is to render the screen in blocks. Anything from 4x4 to 32x32 can produce good results, depending on what effect you want to render. The theory is if you render pixels in a same block one after the other, the corresponding displaced pixels would have a higher probability of being closer together, hence making the cache more efficient. The best thing you can do right now is to test this information for yourself, by implementing a block renderer for the distortion program, and comparing the speed. |
Final words
 |
|
You can now use displacement for virtually anything. For example you could displace the centre of the filtering matrix in last week's fire effect. Bilinear filtering can also be used for most bitmap effects, and definitely worth it if you can put up with slightly worse performance. As for cache efficiency, it is essential to optimise your bitmap effects for cache, since not doing so would severely hinder performance. As for next week, I've no idea what the tutorial will be about. Needless to say that I'd rather surprise you than mislead you ;) You can download this week's demo and source code package right here (132k) Have fun, Alex |